Statistical Process Control (SPC) 從發展到應用至今已經有70年歷史,在1960年左右開始被工業界大量應用。製程能力指標;Cpk;在資訊電子業界早已經廣為人知的東西。
這個指標被用了幾十年,業界人員都如此熟悉,現今Cpk可說是被拿來當做製程是否能符合要求的100%指標。
當製造端遇到製程品質問題待澄清時,常看到用Cpk達標與否來證明製程良劣。
不免俗先來解釋一下Cpk
Cpk是統計分析的產物。因此我們必須從統計的角度去看它。
計算Cpk時,常會聽到量測30個或35個的數量。在統計學裡,當被觀測群體的量很多時,可視為一個服從常態分佈的結果,而抽樣觀察數量>=30。
假設一段製程生產大量的產品,其產品特性的分佈也可以視為常態分佈。
常態分佈圖 (藍線為生產目標,紅線為實際生產狀況)
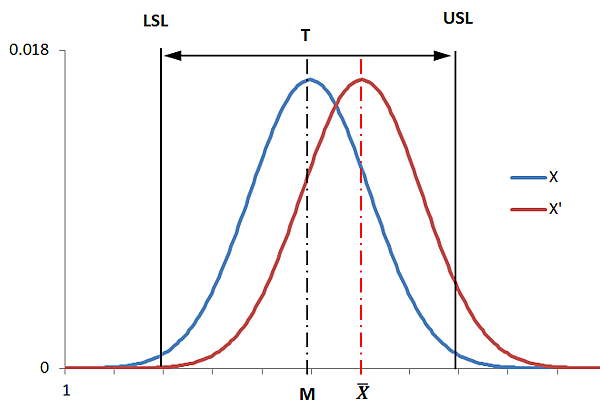
LSL = 產品特性下限
USL = 產品特性上限
M = (USL+LSL)/2
T = USL - LSL
Xbar = 實際產品特性平均值
事實上製程能力指標可以分為三個,分別是Ca、Cp 及 Cpk。
Ca = capability accurency (製程準確度) = (Xbar - μ)/M
Cp = capability precision (製程精密度) = (USL - LSL)/6σ
Cpk = process capability index = Cp * (1-Ca)
可以看得出來,Ca最小值為0,表示實際產品平均落在目標值上,亦即沒有任何偏移。因此 1-Ca 的值會最大。
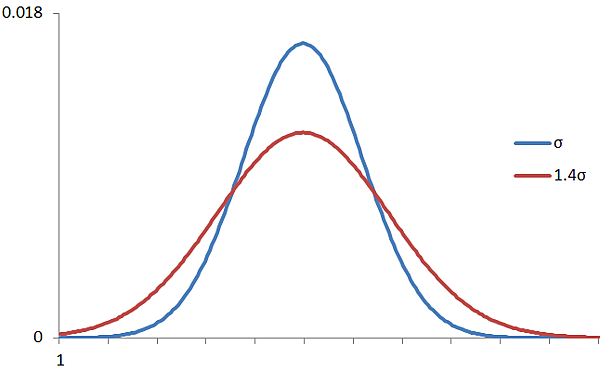
而Cp則可以看出實際產品特性的分佈集中度,分佈越散則標準差越大、Cp越小;分佈越集中則標準差越小、Cp越大。
綜合以上兩點,Cpk值越大表示製程能力越符合我們的目標值。
不同標準差的常態分佈圖 (σ越大則分佈越不集中)
Cpk值對應的處理原則表

直觀以Cpk進行決策的潛在問題
我無意挑戰業界現有的指標,而是在實務上確實會發生Cpk良好,但仍然有高出預期很多的不良現象發生,而且發生不良的特性是在量測數據中的 (也就是在Cpk的控制中)。
在某專案中剛好使用到業界最新規格的module,相關這個module的檢點數;包含結構和電子特性;總共大約有10個。
試產過程中的測試,發現其中兩個檢查點都機會發生失效結果。
我得到的總機台數為65,關於這個module的總檢點數為650。
在相關檢點中發生失效的台數為7台,總失效檢點數為9。
dppm = 13846
經分析後,問題出在module上的兩個重要尺寸超出下限。
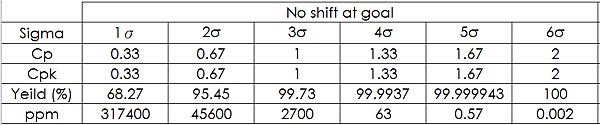
針對這個品質問題,供應商提出製程Cpk給我們參考,以證實其產品的品質。報告上表示這兩個尺寸的 Cpk = 1.34。
在生產目標中心不偏的情況下,Cpk = 1.34 可以對照製程良率至少為 4σ。
而在 4σ 良率的製程及10個檢點數 (我司角度) 來看,良率應該有99.94%
Cpk 對照 6σ 表
檢點數對應 6σ 良率表
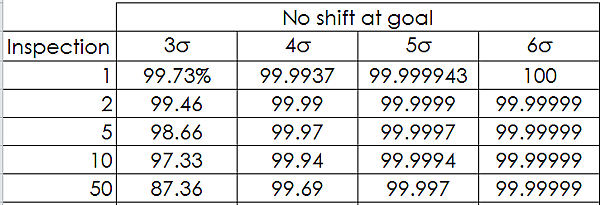
對照實際檢點高達dppm13846,差了23倍,這結果並不科學。
難不成這是準備指摘供應商做假資料的展開嗎?
指標也會有可靠度的下限
事實是,就算延用數十年的指標也會有盲點。
首先,Cpk本身其實是一個預估值,就像可靠度一樣會有上下限的存在,而且其準確性會隨著取樣數及抽樣誤差而變化。
再來,讓我們回顧一下:「製程能力」指的是製程在固定生產條件和穩定管制下所展現出來的生產能力。因此以下兩點是必須具備的:
1. 製程中所有步驟都必須標準化 (SOP)
2. 該製程中各項檢測值都必須在穩定的管制下
SOP是為了標準化所有人為因素,然而該因素是不可能被穩定管制的,參與越多的人為因素Cpk的預估偏差就會越大。
隨著工業4.0的來到,產品開始往量少、變化多的方向走,現在也越來越多生產線引進 cell production 以隨時進行產線變換。但是每次產線變換產品,就是加入一次人為因素的變動。
很多製造商的做法是在新產品進入量產前做一次小量的試產,然後量測Cpk來確定製造能力是否足夠。
公正抽樣的兩個重要條件就是不偏和獨立。以小量試產來量測的Cpk的問題就是:抽樣會一定程度影響其它樣本的獨立性。
假設試產50台,然後抽35台進行量測。抽第一、第二台沒什麼影響,但抽到第20台時,每次抽樣都會限制下次抽樣的範圍,一定程度影響了樣本獨立性。
往往這最後一次決定性的試產,製造都會慎重以待,加上抽樣的獨立性有影響,Cpk的結果都能讓自己滿意。
在以往產線大都是長時間生產的情況下,製造過程中仍會定時抽樣來監控其製程能力指標,試產Cpk只是當成產線是否準備充份邁入量產的指標,對未來持續性的管制並沒有太多決策性的影響。
但隨著市場變化和工業沿革,現在一條產線開下去沒多久就要換產品。(以我目前經驗,遇過有產業是最快2.5小時就換線的)
因此開線只做FAI,至於製程中的Cpk管控就是其次了。即使良率只有2σ,量少,影響不大,該產品可能因製造成本考量照常出貨,也不會做任何立即性的改善。
既然Cpk來自於統計分析法,將一批量的產品視為常態分佈的結果。那麼可以知道:
ξ(t) = (μ - t)/σ
![]()
n = 抽樣數
當給予一固定的可靠度期望值 (1-α) 時
σ上下界限為
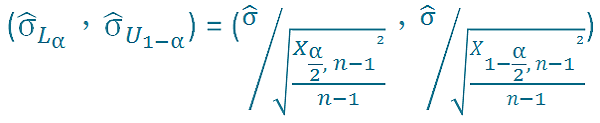
μ 上下界限為
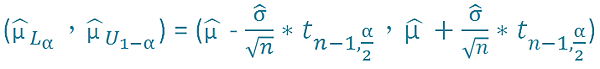
可靠度的估計值為
![]()
由上面可以推知Cpk的估計下限會隨著 ξ 遞減而隨著 n 遞增。
在前面所提到案例裡,該供應商因這個新的module使用的人少,量不多,每生產2000 pcs就停線。
Cpk隨 ξ 遞減而來的影響可視為製程能力的目標中心因某些變因而偏移了。以dppm = 14680 來看,該次的製程能力指標雖然告訴我們其良率為 4σ,但事實上其製程在該次開線時目標中心已經至少偏移了大約T/8 (此數據參考品管先進 ─ 陳文化先生的理論),因此 4σ 的良率<= 97% 而非完全不偏移的 99.94%。
實務上 ξ 不可能得到真實數值,下限偏移量也必須靠繁雜的反覆驗證來求取其極限值,我們沒有閒功夫去推翻供應商提供的Cpk數據。
但換個角度,從抽樣數下手可以確實提高Cpk的準確度。
當產業走到現在這個腳步,產品的母群體數量不再像以往大量生產一樣為未知數,而是一個可預期的數量。
我們可以從母群體的實際數量來推估適合的抽樣數,並利用有效的樣本數來量測該次製造之Cpk會比較有可信度。
有限母體有效樣本數推估
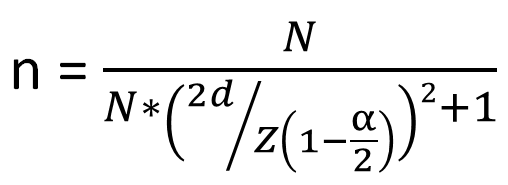
n = 有效抽樣數
N = 母群體數
d = 誤差上限
α = 1-期望可靠度
Z = 常態累積機率
先決定預估的可靠度誤差為10%,可接受的誤差上限為15% (因為此案例中可以接受上限誤差,但不能接受下限誤差,設定能接受誤差為15%表示向下限誤差只容許7.5%),供應商每批量為2000 pcs,則有效抽樣數為60 pcs。
重新要求供應商提供量測數量為 60 pcs 的Cpk結果為1.12,以製造能力中心值不偏的結果來看接近 3σ,而10個檢點數在 3σ 時的製程良率為 97.33%,很接近實際測試中 dppm = 14680的結果。
因此供應商確實是必須要回頭找出問題對製程能力做一些改善。
另外提供以下職涯服務 ─




 留言列表
留言列表

