統計分析 在可靠度裡的重要度在我個人的想法裡應該是越來越重要的。
隨著經濟市場的變化,公司營運成本的降低是非常重要的一環,很多時候可靠度必須要實際驗證來蒐集資料,但是經由統計分析和預估的協助常常可以讓實際測試的樣品數、時間或人力下降,但能得到相當可靠度的結果。例如兩個實驗室在做同樣的測試後產生了矛盾的結果,在排除各種能想到的影響因素後,就得要靠統計方法來分析2組樣品間的異同性後決定是否要再增加測試樣品、或者是增加必要的數量即可。統計的分析應用往往可以幫助我們加速決策的方向並省去決策過程的一些成本。
比較麻煩的就是韋伯機率分佈,尤其是在資源不足的組織裡,要做雙參數的韋伯分布推估實在是一件不太容易的事(三參數太困難,這裡基本上就是要靠軟體)。公司沒有軟體協助,也沒有韋氏機率圖紙可以畫。之前我還特地去找了軟體來參考,像Weibull++買一套就要 USD 2,000+,實在是花不下這個錢。
窮人有窮人的做法,所以我試著利用excel反向繪圖來推估雙參數韋伯分佈。所謂反向繪圖指的是:當利用韋氏機率圖紙來繪圖時,可以直接推估出雙參數的數值,而這個方法則是假設雙參數的值然後繪圖找最接近的曲線。這裡的範例用的是品質學會的教科書例題:某繼電器進行壽命測試的數據如下

我們先驗證數值特低的1283, 1887和數值超過6萬的樣品是否缺乏代表性(α=0.05)。
1283, 1887兩樣本的虛無假設H0=此兩樣本為非早夭,F檢定結果表示可接受H0

同樣驗證62690, 63910, 66888, 73473等樣本的虛無假設H0=此兩樣本為非過長,F檢定結果表示可接受H0

所有樣本結果都具代表性,因此我們把數據輸入,主要取得的數據為ln(t)、累積failure rate。壽命值取ln主要是避免繪圖時橫軸過長。

接下來開始尋找韋伯分佈的雙參數 β 和 θ。
我們先複習一下雙參數韋伯分佈累積失敗機率為F(t)=1-exp[(-t/θ)^β],β 為形狀參數、θ 為特徵壽命(或稱尺度參數)。當 t=θ 時 F(θ)=1-exp(-1)=63.21%。從我們的實際資料中尋找,最接近的數值為sample#31,壽命數據為14833,累積失敗機率為63.27%。因此可以先估算 θ 值為14833。
做第一次評估時,我先假設β值落在1~4之間,則可以把累積失敗機率計算如下:

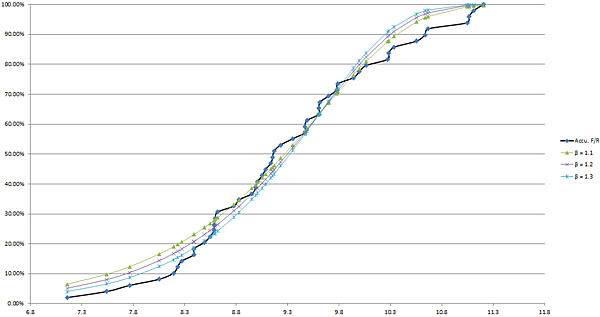
再把這些數據利用XY散佈圖畫出來做和實際測試的累積失敗率比較。可以看出來實際分佈(黑色線)會落在 β 值在1~2之間,而且是比較偏向1。

由於第一次的推估 β = 1~2 且偏向1,因此第二次推估數值的區間設在1~1.5之間為:1, 1.1, 1.2, 1.3, 1.4 及 1.5 。然後重覆上面的手法把F(t)畫出來做比較得到下面的圖。我們可以看出來 β 會比較落在1.1~1.3之間。

把剔除掉不要的值和曲線條給移除掉,留1.1、1.2 及 1.3 來做比較,最接近的值應該會是1.2產生的分布,因此可以推估此雙參數韋伯分布的 β = 1.2,θ = 14833。和教科書上利用韋氏機率圖紙推估出來的結果( β = 1.21 ,θ = 16625.4)做比較,我們利用 excel 繪圖反推的數值其實沒有差太多,再加上繪圖推估法的結果因人而異,多少會有誤差,這樣用反推的方式得到很接近的結論,可用度十分之高。
另外提供以下職涯服務 ─




 留言列表
留言列表

