再談卡方檢定 這個工具在使用上有兩個限制:
1. 卡方檢定中的樣本數不得小於 5 個,或是資料結合後每一格的樣本數不能小於 5。
一般而言,樣本數<5 時必須將樣本合併。或是說格子中的資料不到 5 個時,應該把資料和別格合併。
但事實上,合併資料會使對應的資訊損失。
對於我們從事這種產業的特性來說,很多時候是不可能取得大樣本的資料的。
2. 樣品太少不適合使用卡方檢定,相反,樣本太多也不行。
首先,卡方統計量是「近似」卡方分配。在樣本太少時近似的結果並不準確。
其次,當樣本數太大時,卡方統計量會一下子爆增很多,例如自由度 60,顯著水準為97.5% 時卡方統計量為 83.298。
大樣本雖然好,但卡方檢定變得太過敏感,檢定起來反而沒意義。
─ 葉茲連續校正 ─
先喚醒對卡方檢定的計憶,在談卡方分配時提到過,利用二維表進行檢定時,卡方統計量為

1934 年 Yates (依國家教育研究院雙語詞彙翻譯為葉茲)提出了卡方檢定的校正量,使卡方統計量為
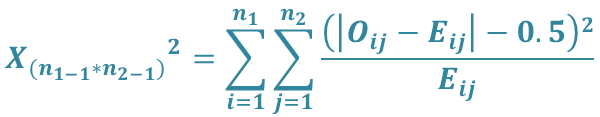
這只是一個小變動,但帶來意外大的結果。
在 C Stefansecu 的著作 Yates’s Continuity Correction 中它提出了一個數據來顯示葉茲連續校正的效果
Yates’s Continuity Correction (London Business School, C Stefansecu)
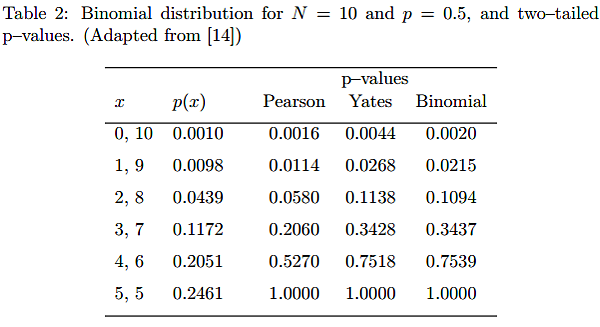
Stefansecu 設計了一個實驗機率為 0.5 (二項次分佈),次數為 10 次的實驗結果。
從這個數據會發現葉茲連續校正的結果十分接近真實的雙尾機率 (Binomial)。
比較圖
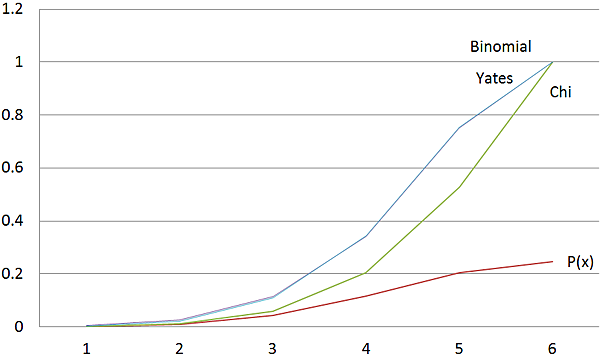
由這個比較結果可以看出葉茲提出的這個校正結果明顯比卡方檢定貼近實際結果。
Yates 指出:卡方分配為一個連續性的分佈,所以對於間斷的資訊只能得到一個近似的結果。從這個角度來看,也可以發現這是為什麼樣本數太少時,卡方檢定的表現結果會不如預期。同時這也是這個公式被稱為「連續」校正的原因。
但葉茲連續校正有著巨大的缺陷,也就是超過 2X2 的二維表,這個公式就不再適用了。
另外,葉茲連續校正的公式在後續的研究者持續研究下,也被認為過於保守。
過於保守指的是錯誤率 (p) 顯然小於顯著水準。雖然降低了型 I 的錯誤機率,但在全機率不變的情況下,型 II 的錯誤機率就提升了。
型 I 及型 II 錯誤示意
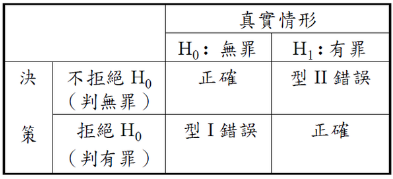
舉個通俗點的例子。
固然法官不小心把無罪判成有罪是十分可怕的,所以 H0 一向都是以「難以推翻」為假設,也就是無罪推定。因此控制顯著水準是要控制錯把無罪判有罪的機率。但若因此而讓法官都太過小心,提高了把有罪判成無罪的可能性,那結果也沒比較好。這就像現今台灣的司法困境。
第三,葉茲連續校正只適合做單尾檢定。在雙尾的狀況下,過度保守的狀況又再出現,使得 H0 幾乎無法被推翻,檢定也變得沒有意義。
在 1967 年開始有統計學家提出意見,指出 Yates 的公式無法推展到所有狀況,只能視為一種為了近似二項分佈和超幾何分配的修正特例。
這中間我們可以看出統計學家間的歧見,在於「假定資料的背後隱含著某種分配」。這也是卡方分配的發明人 Karl Pearson 和 Yule 爭執的原因。
Yule 認為類別變數是離散的,但 Pearson 認為在交叉表的背後存在著某種連續分配。
我想,這個問題永遠缺乏答案,因為在時間和成本的許可下,我們總是只能利用抽樣結果,無論抽樣數是 10 或 1000,而母體永遠是無法被絕對探知的。現代統計中會發現各派支持的學家都有,也因此形形色色的統計模型工具也會使用不同的假定,不同的假定下計算得到的結果也不盡相同。
就像在電視上看到候選人/政黨支持度的名調時,總會有人跳出來質疑抽樣幾百人就想代表上百萬人的結果。
曾經有位同事就告訴我,當我試著用統計方法解決問題時,很可能這個問題並不是如我所預期的分佈。
這句話至今我仍銘記在心。
只是隨著多年的辯論和發展,各派皆有其優缺點,我只能借助一百多年來大師們的經驗進行評估而已。
─ 費雪精確檢定 ─
Fisher 和 Yates 間不只是師徒的關係,更是長期以來在統計學上的合作伙伴。
Yates 的連續校正公式雖然遭受許多批評,但他和 Fisher 合力針對交叉表的小樣本檢定發表了多次精確檢定的內容。對 Fisher 來說,他在後續對精確檢定的推廣和影響力上,都受到 Yates 在背後的許多幫助。
從前面看得出來, Yates 對假定資料背後隱含的分配意見不同於 Pearson。Fisher 跟 Yates 一樣也是站在 Yule 角度。
Fisher 提倡的精確檢定有著二元超幾何分配的性質,適用 2x2 二維表。一旦超過,就會變成多元超幾何分配,這點最後再談。
超幾何分配探討的是「取後不放回」的情境,而連續分配談的則是「取後放回」。
比較一下二項分配和二元超幾何分配:
有一桶子裝白球 x 3,紅球 x 5
1. 二項分配 - 每次取一球後放回,連續四次,1 白 3 紅的機率
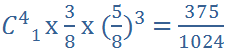
2. 二元超幾合分配 - 每次取一球後不放回,連續四次,1 白 3 紅的機率
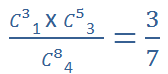
在大樣本的情境下,二項分配的期望值和變異數就等於二元超幾何分配,但在小樣本的狀況下就會顯示出差異。
因此超幾何分配是用來探討有限母體的狀況。
1935 年 Fisher 用了一個知名的「品茶實驗」來說明精確檢定。
近代下午茶發展自英國維多利亞時代,一開始是貴族用來打發下午時光。英國下午茶不必然有豐盛的食物,但茶是通常都有的。
1920 年代後期,有天下午一位女仕對眾科學家宣稱:奶茶調製的順序有很大的影響。把奶加進茶裡和把茶加進奶裡,二者喝起來口味大不相同。當然所有的科學家都十分不屑,畢竟 a+b = b+a。但 Fisher 可不做如此想,他十分當一回事,並設計了一個實驗來檢定她的說法,這就是有名的 lady testing tea。
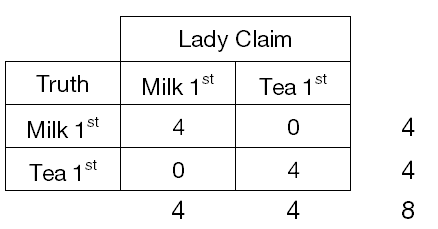
假設 Fisher 用了 8 杯茶來測試,其中 4 杯先放奶另外 4 杯先放茶。
則 H0 定義為「不能判斷」或是以卡方獨立檢定的角度來看「猜測杯數和實際杯數互相獨立」。
必須重新強調前面提到的判斷錯誤,H0 是必須被保護的,就像無罪推定一樣。所以虛無假設是被定義為不能判斷,但如果我們能推翻H0,就可以大聲宣告試驗結果是真的能被判斷。
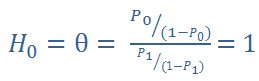
![]()
當試驗結果,女仕在「先放奶/茶的 4 杯中正確猜出 3 杯」時,
4杯猜對3杯
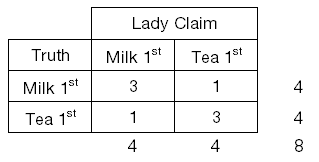
則這個結果的機率為
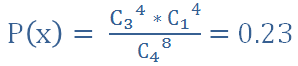
如果我們要判斷女仕是否真的能猜對,則猜對大放猜錯的機率再加上「4杯完全猜對」
4杯猜對4杯
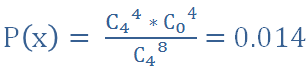
「猜對大於猜錯」的「正確」機率為 0.23+0.014 = 0.244。
這不是近似結果,而是真正的顯著水準。
所以如果女仕猜對了 3 杯,我們可以精確檢定出顯著水準為 0.23,落入拒絕域中。我們可以說猜對的杯數和實際杯數「不獨立」,也就是有正相關性。
這也是精確檢定這個名稱的由來,因此它估算的真正的機率而非近似值。
然而計算間斷資料的缺點就在放計算過程太過繁雜。
在品茶實驗中的交叉表是 2x2,但如果今天要檢驗的是有數十種可能性,那可以想見計算的複雜度。
也因此在當時,Fisher 不得不承認只要樣本數不會過小,還是應該執行卡方檢定。
在小樣本的情況下,Yates 連續校正公式在計算上是比 Fisher 精確檢定來得快速。但在現代電腦效能提升的狀況下,即使是大樣本,Fisher 精確檢定的計算已經成為可能,所以 Yates 的公式在現代已經沒有人在使用。
另外提供以下職涯服務 ─




 留言列表
留言列表

